Railway Train Braking Concepts
Introduction to Train Braking – 1
- Initially braking was available only from locomotive and other vehicles on freight trains were unbraked.
- In UK it was a legal requirement to fit continuous brakes on Passenger trains.
- Vacuum brakes were initially dominant; their principal advantage was that they were easy to engineer to be “fail-safe” and therefore relatively cheap. Brakes were applied by gravity unless a pipe running the length of the train was exhausted of air by an ejector, and on a steam locomotive this required a device with no moving parts which was a decided advantage. Loss of vacuum in the train pipe provided an automatic braking action on both portions of a train should it become divided. Once the brake is applied release require re creation of vacuum.
- Air brake have the advantage of higher performance “two-pipe system” – the reservoir pipe provides a constant source of compressed air down the length of the train completely separate from the train pipe which controls the braking. Reduced delay occurs during release of brakes
Introduction to Train Braking – 2
- Electro-Pneumatic brake utilises electrical control rather than the air pipe to control the brake application on each vehicle. The great advantage is that brakes are applied by electrically operated valves and thus the response is immediate and simultaneous on all vehicles on a train, rather than gradually from the front end as the loss of air pressure gradually percolates along the train pipe. One disadvantage is that the electrical system by itself could not be completely failsafe.
- Modern trains generally use an electronic variant of the Electro-Pneumatic brake but with a train wire all around the train taking the role of the train air pipe to prove the train intact and provide an automatic brake application if the circuit is broken. The brakes are also more sophisticated in that the braking force on each vehicle is adjusted according to its loading as determined from measuring the weight on the suspension.
Introduction to Train Braking – 3
- Many types of rolling-stock on Network Rail have 3-step service braking nominally equivalent to 3%g mean, 6%g mean, and 9%g mean, where g is the acceleration due to gravity of approximately 9.81 ms-2 (i.e. an increase of speed of 9.81 metres per second, every second). A driver braking for a speed restriction would be expected to use the most severe braking (step 3 which equates to 0.88 ms-2) whereas defensive driving policy for approaching a signal at danger would utilise step 2 (equates to 0.58 ms-2) for the final part of the approach in order to have some braking in reserve. If step 3 is used drivers are often required to inform the maintenance staff since it is possible that its use has resulted in noticeably higher wear of brake components than would normally be expected.
- There is also an emergency brake which should be no less than step 3; it is often significantly sharper and many trains achieve 12%g (1.17 ms-2).
Braking Rates
- The limiting factor for the brake rate is often the available adhesion; there is a relatively small area of contact between wheel and rail. In poor rail head conditions, the co-efficient of friction can be less than 10% its normal value. In these circumstances it is likely that the wheel will slide along the rail rather than continuing to rotate. This must be avoided as it both results in a loss of braking and causes a “flat” on the wheel and if such a damaged wheel is allowed to continue in service it results in a hammer blow on the track, itself causing rail damage and passenger discomfort. Hence modern rolling stock features WSP (=Wheel Slip Protection) which briefly releases the brakes on the axle so that it revolves again.
Today’s freight trains are very much heavier and travel at considerably higher speeds and therefore must have far more effective brakes than the traditional railway freight
Braking Technique
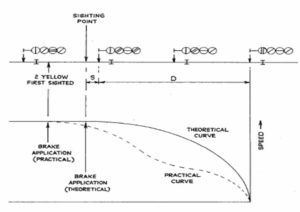
- Signalling calculations assume that a brake application is uniform from the point of application at the sighting point to the train coming to the rest at the Signal.
- The assumption of a constant brake application is a gross simplification. When train is running at high speed, the driver tends to brake in two stages (or more)
- First driver makes a limited application well on the approach side of sighting point, then when the train speed has been reduced to roughly half of original value, he eases the application ; and finally he makes a heavier one to bring the train to a stand.
- The time taken to bring the train to rest is about the same as it would be with a uniform application. Therefore this assumption is frequently used for headway calculations.
Theoretical and Practical Braking
Braking Distance Calculations
- There are two possible ways in which the braking distance of any train could be determined:
- Theoretical assessment of the braking rate which can be achieved by the trains’ design and use of Newton’s Laws of motion to determine the distance travelled during braking from any given initial speed and adjusted accordingly for the effects of gradient (method favoured by the London Underground and by many continental administrations),
- A series of physical trials with differing loads, speeds and gradients in order to give a practical set of braking distances (method favoured historically by British Rail and the origin of the braking tables and curves).
- There are two possible ways in which the braking distance of any train could be determined:
- Theoretical assessment of the braking rate which can be achieved by the trains’ design and use of Newton’s Laws of motion to determine the distance travelled during braking from any given initial speed and adjusted accordingly for the effects of gradient (method favoured by the London Underground and by many continental administrations),
- A series of physical trials with differing loads, speeds and gradients in order to give a practical set of braking distances (method favoured historically by British Rail and the origin of the braking tables and curves).
Braking Distance Calculations -2
- It is obviously important that there is a high degree of certainty that braking can be achieved within the specified distance under any reasonably foreseeable circumstances. Hence allowances are made for such factors as:
- Poor weather conditions.
- Driver’s reaction times to a warning.
- Driver’s slight misjudgement of brake application.
- System reaction time to a brake application Variations in a standard braking system from train to train, (e.g. as a result of normal wear in the equipment, brakes having needed to be isolated on a vehicle of the train)
- Hence the published information resulting from either the theoretical or the empirical method incorporates a safety margin.
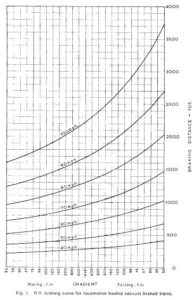
Braking Distance Curves
- Each line on the graph is a braking curve which shows how the braking distance for any particular speed depends upon the gradient of the line.
- The different lines are the braking curves for different speeds;
- To a first approximation, the distance required to stop is proportional to the square of the speed.
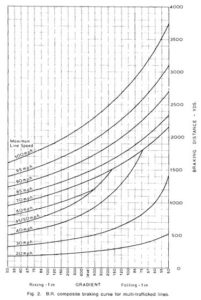
Composite B.D. Curves
- The braking performance of different types of trains varies greatly, there being particularly marked differences between passenger coaches and freight vehicles which, being significantly heavier, have more kinetic energy at any given speed and generally fewer axles on which braking can be applied for a given weight. Hence the need for “composite curves” as shown here where the higher speed curves are the same as before (the freight does not run at those speeds) but the freight curves are applicable at the slower speeds as their braking distances are greater.
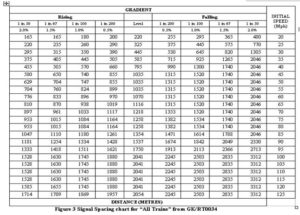
Braking Tables
- Another way of presenting the same braking distance information is in a braking table, such as that shown below. Although less easy to visualise than a braking chart, it can be read consistently, avoiding the need for interpolation. Sometimes such tables do not have entries as close as in multiples of 5mph; if actual initial speed is not included in the presentation then necessary always choose the next higher speed that is shown in the table.
- The distance given in the table above is an absolute minimum for signalling design. It does however already include sufficient contingency to cover eventualities such as adverse weather conditions, permitted degradation of a train’s braking ability. It is the interface specification between rolling-stock engineering and signal engineering.
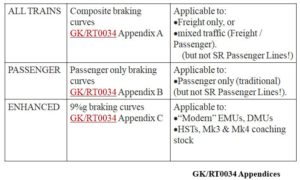
Selection of Applicable Braking Curves
Whenever use is made of braking tables or braking curves it is important to ensure that the information relates to the correct variety of train being considered. On a mixed traffic railway it is important that the braking distances provided are adequate for all types of trains that are permitted on the line so that they can brake to a stand from their authorised speed within the available.
Historically this would have been a question of using the “All Trains” curves rather than the “Passenger Only” curves.
Nowadays passenger traffic generally dominates; the relatively small amount of remaining freight which has also changed significantly in nature. Hence the signalling is generally optimised for passenger traffic of the fastest trains using the line and in order that traffic with less effective braking can still use the line safely, it is necessary to impose differential speed limits. It is important to realise that this does often result in these other train operating at slower speeds than would otherwise be the case and this, in turn, affects headway and leads to a loss of line capacity that can itself have detrimental effects on the faster traffic.
Selection of Applicable Braking Curves – 2
Braking Distance Calculations
where:
a = acceleration (ms-2)
v = final velocity (ms-1)
u = initial velocity (ms-1)
s = distance (m)
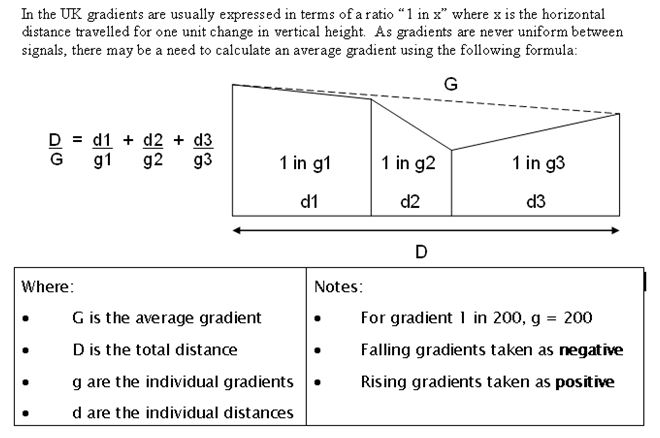
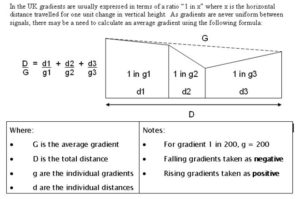
Average Gradient
Effect of Gradient on Braking
It is probably easiest to consider a stationary train left with no brakes applied whilst standing on a line of constant gradient. Gravity exerts a downwards force proportional to the mass of the train, the vast majority of which is perpendicular to the rails. However there is a small component of that force which is parallel to the rails since the line at this place is not exactly level. Hence this force acts to accelerate the train along the line in the downhill direction; this produces an acceleration.
For a moving train gradient has exactly the same effect, so:
- for a train travelling uphill then its effective retardation rate will be the sum of its inherent braking and that due to gravity thus reducing its stopping distance, whereas
- for a train travelling downhill then its effective retardation rate is lessened due to the effects of gravity and the stopping distance extended.
Railway Train Braking Concepts,Introduction to Train Braking,Braking Rates,Braking Technique,Theoretical and Practical Braking,Braking Distance Calculations,Braking Distance Curves,Composite B.D. Curves,Braking Tables,Selection of Applicable Braking Curves,Braking Distance Calculations,Effect of Gradient on Braking
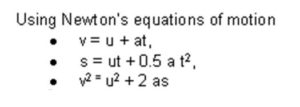




I tried to make a patent application on a railway breaking system, only to find an similar system is already patented, for some reason these systems are not being applied as it would greatly reduce the stopping distance?